1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
C++로 작성한 백준 문제 1074번 Z에 대한 문제 풀이다.
분할정복 문제로 수학적 추론이 문제를 푸는데 필요한 주요 지식이다.
문제 설명
문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
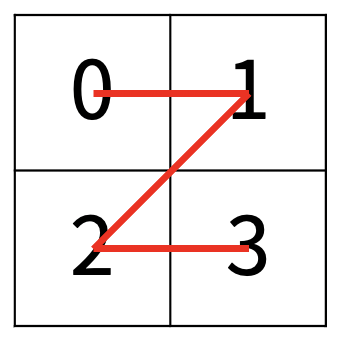
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
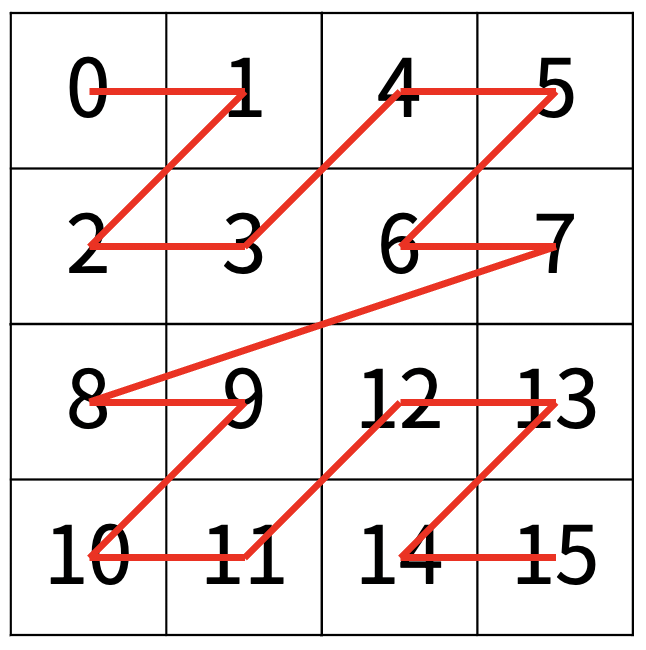
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.
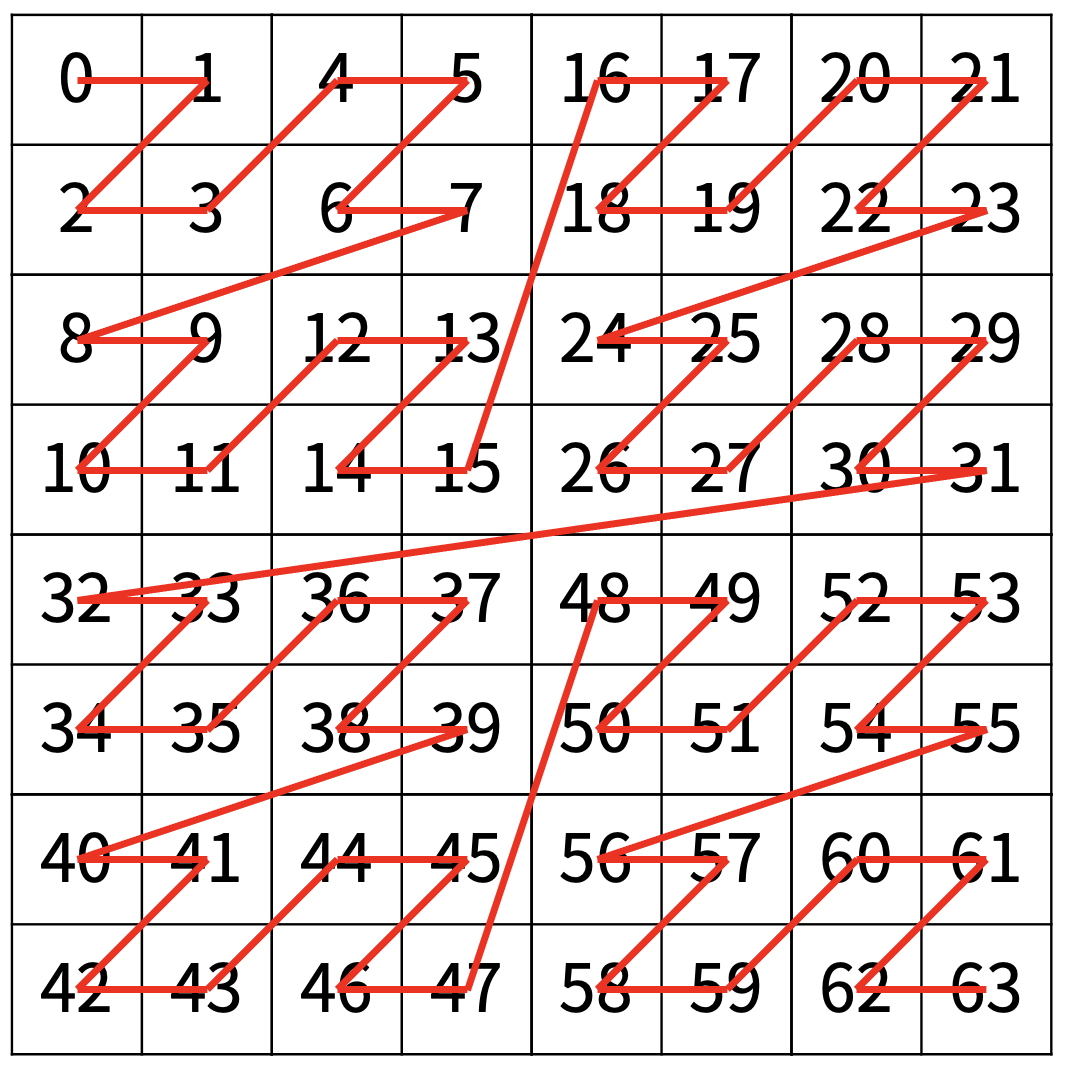
입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
제한
- 1 ≤ N ≤ 15
- 0 ≤ r, c < 2N
문제 파악하기
- 사각형 내에서 숫자 패턴이 반복되는 것을 찾아야 한다.
- 가로줄 따로 세로줄 따로 기준으로 숫자가 어떨때 얼만큼 증가하는지 파악해야 한다.
- 사각형이 확장되면서 숫자가 증가하므로 이진수를 이용해 값을 변환하고 계산하면 된다.
코드 및 설명
#include <iostream>
#include <math.h>
#include <bitset>
#define fastio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
int N, R, C;
int binary(long long r){
int binary[18];
int position = 0;
long long advantage =0;
while (1)
{
binary[position] = r % 2; // 2로 나누었을 때 나머지를 배열에 저장
r = r / 2; // 2로 나눈 몫을 저장
position++; // 자릿수 변경
if (r == 0){ // 몫이 0이 되면 반복을 끝냄
break;
}
}
for (int i = position - 1; i >= 0; i--)
{
if(binary[i]==1){
advantage+=pow(2,2*i+1);
}
}
return advantage;
}
int binary2(long long r){
int binary2[18];
int position2 = 0;
long long advantage2 =0;
while (1)
{
binary2[position2] = r % 2; // 2로 나누었을 때 나머지를 배열에 저장
r = r / 2; // 2로 나눈 몫을 저장
position2++; // 자릿수 변경
if (r == 0){ // 몫이 0이 되면 반복을 끝냄
break;
}
}
for (int i = position2 - 1; i >= 0; i--)
{
if(binary2[i]==1){
advantage2+=pow(2,2*i);
}
}
return advantage2;
}
int main(){
fastio;
cin>>N>>R>>C;
cout<<binary(R)+binary2(C);
return 0;
}
- binary() 함수는 세로를, binary2() 함수는 가로를 처리해준다. 둘의 구성은 거의 비슷하다.
- 둘다 받은 index를 이진수로 변환하고 그 이진수에 맞게 계산해준다.
- 먼저 index를 이진수로 변환한다. 그리고 다음과 같은 규칙을 적용하면 된다.
| 2진수가 1인 위치 | 세로에서 누적되는 값 | 가로에서 누적되는 값 |
| 0 | +2 | + 1 |
| 1 | + 8 | + 4 |
| 2 | + 32 | + 16 |
| 3 | + 128 | + 64 |
| 4 | + 512 | + 256 |
| 5 | + 2048 | + 1024 |
| ... | ... | ... |
- 즉 값을 2진수로 변환한 다음 1인 위치를 i라고 할때 세로면 2^(2i+1) 가로면 2^2i 만큼 누적시켜주면 된다.
- 값의 범위가 크므로 출력할때 outofbound에러나 overflow가 나지 않도록 해야한다.
헤매었던 부분
- 이진수 계산을 어떤 방식으로 할지 고민하였다. bitset을 쓸까 아니면 비트 시프트연산자를 쓸까하다가 둘다 익숙지 않고, N의 크기가 그렇게 크지 않아 그냥 for문으로 처리하였다.
- for문으로 이진수로 바꾸는 과정에서도 더 효율적인 방법이 있었는데 역순으로 계산하다가 시간이 조금 걸렸다.
마무리
반복되는 패턴을 찾아야 하는 문제였다. 재귀적으로도 풀 수 있었으나 더 빠르게 수학적으로 푸는 방법을 택했다.
'algorithm > math' 카테고리의 다른 글
| [백준] 18110번: solved.ac 풀이 및 해설(C++) (0) | 2024.01.18 |
|---|
1074번: Z
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다. N > 1인 경우, 배열을
www.acmicpc.net
C++로 작성한 백준 문제 1074번 Z에 대한 문제 풀이다.
분할정복 문제로 수학적 추론이 문제를 푸는데 필요한 주요 지식이다.
문제 설명
문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.

N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.

N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.

입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
제한
- 1 ≤ N ≤ 15
- 0 ≤ r, c < 2N
문제 파악하기
- 사각형 내에서 숫자 패턴이 반복되는 것을 찾아야 한다.
- 가로줄 따로 세로줄 따로 기준으로 숫자가 어떨때 얼만큼 증가하는지 파악해야 한다.
- 사각형이 확장되면서 숫자가 증가하므로 이진수를 이용해 값을 변환하고 계산하면 된다.
코드 및 설명
#include <iostream>
#include <math.h>
#include <bitset>
#define fastio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
int N, R, C;
int binary(long long r){
int binary[18];
int position = 0;
long long advantage =0;
while (1)
{
binary[position] = r % 2; // 2로 나누었을 때 나머지를 배열에 저장
r = r / 2; // 2로 나눈 몫을 저장
position++; // 자릿수 변경
if (r == 0){ // 몫이 0이 되면 반복을 끝냄
break;
}
}
for (int i = position - 1; i >= 0; i--)
{
if(binary[i]==1){
advantage+=pow(2,2*i+1);
}
}
return advantage;
}
int binary2(long long r){
int binary2[18];
int position2 = 0;
long long advantage2 =0;
while (1)
{
binary2[position2] = r % 2; // 2로 나누었을 때 나머지를 배열에 저장
r = r / 2; // 2로 나눈 몫을 저장
position2++; // 자릿수 변경
if (r == 0){ // 몫이 0이 되면 반복을 끝냄
break;
}
}
for (int i = position2 - 1; i >= 0; i--)
{
if(binary2[i]==1){
advantage2+=pow(2,2*i);
}
}
return advantage2;
}
int main(){
fastio;
cin>>N>>R>>C;
cout<<binary(R)+binary2(C);
return 0;
}
- binary() 함수는 세로를, binary2() 함수는 가로를 처리해준다. 둘의 구성은 거의 비슷하다.
- 둘다 받은 index를 이진수로 변환하고 그 이진수에 맞게 계산해준다.
- 먼저 index를 이진수로 변환한다. 그리고 다음과 같은 규칙을 적용하면 된다.
| 2진수가 1인 위치 | 세로에서 누적되는 값 | 가로에서 누적되는 값 |
| 0 | +2 | + 1 |
| 1 | + 8 | + 4 |
| 2 | + 32 | + 16 |
| 3 | + 128 | + 64 |
| 4 | + 512 | + 256 |
| 5 | + 2048 | + 1024 |
| ... | ... | ... |
- 즉 값을 2진수로 변환한 다음 1인 위치를 i라고 할때 세로면 2^(2i+1) 가로면 2^2i 만큼 누적시켜주면 된다.
- 값의 범위가 크므로 출력할때 outofbound에러나 overflow가 나지 않도록 해야한다.
헤매었던 부분
- 이진수 계산을 어떤 방식으로 할지 고민하였다. bitset을 쓸까 아니면 비트 시프트연산자를 쓸까하다가 둘다 익숙지 않고, N의 크기가 그렇게 크지 않아 그냥 for문으로 처리하였다.
- for문으로 이진수로 바꾸는 과정에서도 더 효율적인 방법이 있었는데 역순으로 계산하다가 시간이 조금 걸렸다.
마무리
반복되는 패턴을 찾아야 하는 문제였다. 재귀적으로도 풀 수 있었으나 더 빠르게 수학적으로 푸는 방법을 택했다.
'algorithm > math' 카테고리의 다른 글
| [백준] 18110번: solved.ac 풀이 및 해설(C++) (0) | 2024.01.18 |
|---|
