[알고리즘] 4. Transform and Conquer 내용 정리
[알고리즘] 3. Decrease and Conquer 내용 정리
1. Brute force2. Divide and conquer3. Decrease and conquer4. Transform and conquer5. Greedy Method6. Dynamic Programming7. Backtracking8. Branch and Bound여기서는 Decrease and conquer에 대해 다룬다.Decrease and Conquer란주어진 문
juneforpay.tistory.com
1. Brute force
2. Divide and conquer
3. Decrease and conquer
4. Transform and conquer
5. Greedy Method
6. Dynamic Programming
7. Backtracking
8. Branch and Bound
여기서는 Transform and conquer 에 대해 다룬다.
Transform and Conquer란
문제를 해결하기 위해서 풀기 쉬운 형태로 바꾼다. 그런 후 그 새로운 문제를 푸는 방식이다.
Transform and conquer 예시
- 문제 요소를 어떻게 바꾸는 지에 따라 3가지로 분류 할 수 있다.
- Simpler instance : 더 간단한 인스턴스로 변형
- Presorting
- Gaussian Elimination
- Another representation: 표현 방식의 변경
- Balanced Search Trees (AVL, Red-Black)
- multiway balanced Trees (2-3 trees, B trees)
- HeapSort
- Another problem's instance: 다른 문제의 해결방법 적용
- Computing Least common Multiple
Presorting
#include <iostream>
#include <vector>
#include <algorithm>
#include <chrono>
#include <cstdlib>
using namespace std; // std 네임스페이스를 사용
using chrono::high_resolution_clock;
using chrono::duration;
using std::vector;
using std::cout;
using std::endl;
// Brute Force 방식
vector<int> brute_force_remove_duplicates(const vector<int>& arr) {
vector<int> result;
for (size_t i = 0; i < arr.size(); ++i) {
bool is_duplicate = false;
for (size_t j = 0; j < result.size(); ++j) {
if (arr[i] == result[j]) {
is_duplicate = true;
break;
}
}
if (!is_duplicate) {
result.push_back(arr[i]);
}
}
return result;
}
// Presorting 방식
vector<int> presorting_remove_duplicates(vector<int>& arr) {
sort(arr.begin(), arr.end()); // 먼저 정렬
vector<int> result;
for (size_t i = 0; i < arr.size(); ++i) {
if (i == 0 || arr[i] != arr[i - 1]) {
result.push_back(arr[i]);
}
}
return result;
}
int main() {
// 30000개의 랜덤 배열 생성
vector<int> arr(30000);
for (int &num : arr) {
num = rand() % 10000 + 1; // 1부터 10000까지의 랜덤 숫자
}
// Brute Force 방식 실행 시간 측정
auto start_time = high_resolution_clock::now();
brute_force_remove_duplicates(arr);
auto end_time = high_resolution_clock::now();
duration<double> brute_force_duration = end_time - start_time;
cout << "Brute Force 방식 실행 시간: " << brute_force_duration.count() << "초" << endl;
// Presorting 방식 실행 시간 측정
start_time = high_resolution_clock::now();
presorting_remove_duplicates(arr);
end_time = high_resolution_clock::now();
duration<double> presorting_duration = end_time - start_time;
cout << "Presorting 방식 실행 시간: " << presorting_duration.count() << "초" << endl;
return 0;
}- 무작위 수들이 들어있는 배열에서 중복된 수들을 제거해야할때 쓸 수 있다.
- 그냥 bruteforce로 할때보다 Presorting으로 미리 정렬하고 시작하면 훨씬 시간을 절약 할 수 있다.
- 랜덤 수열에서 가장 빈도가 높은 수를 찾는데에도 이용할 수 있다.
- 많은 기하학 알고리즘에서도 우선 점들을 거리나 각도에 따라 미리 index를 붙여 정렬하는 방식을 사용한다.
Gaussian elimination
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
// 함수: 행렬을 출력
void printMatrix(vector<vector<double>>& matrix) {
for (const auto& row : matrix) {
for (double val : row) {
cout << val << "\t";
}
cout << endl;
}
}
// 함수: 가우시안 엘리미네이션
void gaussianElimination(vector<vector<double>>& matrix) {
int n = matrix.size(); // 행렬의 크기 (변수의 수)
// 가우시안 엘리미네이션을 통해 상삼각형 행렬로 변환
for (int i = 0; i < n; ++i) {
// 피벗 행렬로 주어진 행의 값을 1로 만들어줌 (정규화)
double pivot = matrix[i][i];
//그러고 나서 그 식의 나머지 값들 다 맞춰줌. 즉 계수를 약분하는 과정임.
for (int j = 0; j < n + 1; ++j) {
matrix[i][j] /= pivot;
}
// 아래 행들에 대해 0을 만들기
for (int j = i + 1; j < n; ++j) {
double factor = matrix[j][i];
// 바로 위의 값과 맞추어 소멸할 수 있도록 하는 계수 factor
for (int k = 0; k < n + 1; ++k) { //k는 n번째 값 즉 = 다음의 상수항까지도 계산
matrix[j][k] -= factor * matrix[i][k];
}
}
}
}
// 함수: 후방 대입 (Back Substitution)
vector<double> backSubstitution(vector<vector<double>>& matrix) {
int n = matrix.size();
vector<double> solution(n);
// 뒤에서부터 해를 구함
for (int i = n - 1; i >= 0; --i) {
solution[i] = matrix[i][n]; // 마지막 열이 상수항
for (int j = i + 1; j < n; ++j) {
solution[i] -= matrix[i][j] * solution[j];
}
}
return solution;
}
int main() {
int n;
cout << "Enter the number of variables (n): ";
cin >> n;
vector<vector<double>> matrix(n, vector<double>(n + 1));
// 사용자로부터 계수와 상수항 입력받기
cout << "Enter the coefficients and constant terms for each equation:" << endl;
for (int i = 0; i < n; ++i) {
cout << "Equation " << i + 1 << ": ";
for (int j = 0; j < n; ++j) {
cin >> matrix[i][j]; // 계수 입력
}
cin >> matrix[i][n]; // 상수항 입력
}
// 가우시안 엘리미네이션으로 상삼각행렬로 변환
gaussianElimination(matrix);
// 변환된 행렬 출력
cout << "\nUpper triangular matrix after Gaussian elimination:" << endl;
printMatrix(matrix);
// 후방 대입을 통해 해 구하기
vector<double> solution = backSubstitution(matrix);
// 해 출력
cout << "\nSolution:" << endl;
for (int i = 0; i < solution.size(); ++i) {
cout << "x" << i + 1 << " = " << solution[i] << endl;
}
return 0;
}- 항이 여러개인 연립방정식을 쉽게 계산하기 위해 나온 방법이다.
- 행렬로 표현된 연립방정식을 역삼각행렬로 만든다.
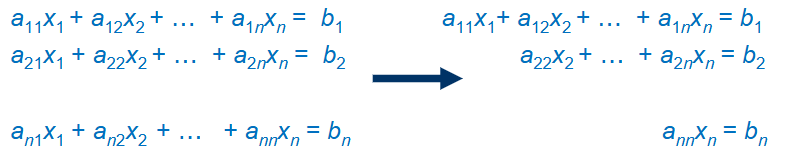
1-1) 첫째식의 첫째항 계수(a11)를 1로 만든다고 생각하고 식의 모든 항을 a11로 나누어 준다.
1-2) 둘째식의 첫째항 계수(a21)를 -1로 만든다 생각하고 식의 다른 모든 항을 -a21로 나누어 준다.
1-3) 그리고 둘째식을 첫번째 식과 더해 그 값으로 둘째식을 기록한다. 이러면 a21은 사라진다.
1-4) 그리고 셋째식, 넷째식... 쭉 반복하여 모든 식의 an1 값을 제거해준다.
1-5) 같은 원리로 이번에는 둘째식과 셋째식의 a22와 a32를 비교하여 a32를 없애주는 방식으로 처리한다.
1-6) 이하 같은 원리를 사용한다. 즉 a11에 맞추어 a21~ an1 을 제거하고, a22에 맞추어 a32~an2를 제거하여 ann까 지 반복하는 것이다.
2. 역삼각행렬을 만들었으면, 이제 가장 아래부터 값이 나온다. 그 값들을 아래서부터 위로, 오른쪽에서 왼쪽으로 값을 대 입해가며 구할 수 있다.
AVL Tree
#include <iostream>
#include <algorithm>
using namespace std;
class AVLTree {
public:
struct Node {
int value;
Node* left;
Node* right;
int height;
Node(int val) : value(val), left(nullptr), right(nullptr), height(1) {}
//생성자
};
Node* root;
AVLTree(Node* rootNode) : root(rootNode) {}
int height(Node* node) {
return node ? node->height : 0;
}
int balanceFactor(Node* node) {
return height(node->left) - height(node->right);
}
void updateHeight(Node* node) {
node->height = max(height(node->left), height(node->right)) + 1;
}
Node* leftRotate(Node* node) {
Node* newRoot = node->right;
node->right = newRoot->left;
newRoot->left = node;
updateHeight(node);
updateHeight(newRoot);
return newRoot;
}
Node* rightRotate(Node* node) {
Node* newRoot = node->left;
node->left = newRoot->right;
newRoot->right = node;
updateHeight(node);
updateHeight(newRoot);
return newRoot;
}
Node* balance(Node* node) {
updateHeight(node);
if (balanceFactor(node) > 1) {
if (balanceFactor(node->left) < 0) {
node->left = leftRotate(node->left);
}
return rightRotate(node);
}
if (balanceFactor(node) < -1) {
if (balanceFactor(node->right) > 0) {
node->right = rightRotate(node->right);
}
return leftRotate(node);
}
return node;
}
Node* minValueNode(Node* node) {
Node* current = node;
while (current->left) current = current->left;
return current;
}
Node* deleteNode(Node* root, int value) {
if (!root) return root;
if (value < root->value) {
root->left = deleteNode(root->left, value);
} else if (value > root->value) {
root->right = deleteNode(root->right, value);
} else {
if (!root->left || !root->right) {
Node* temp = root->left ? root->left : root->right;
delete root;
return temp;
}
Node* temp = minValueNode(root->right);
root->value = temp->value;
root->right = deleteNode(root->right, temp->value);
}
return balance(root);
}
void deleteValue(int value) {
root = deleteNode(root, value);
}
void inorderTraversal(Node* node) {
if (!node) return;
inorderTraversal(node->left);
cout << node->value << " ";
inorderTraversal(node->right);
}
void printTree() {
inorderTraversal(root);
cout << endl;
}
};
int main() {
AVLTree::Node* root = new AVLTree::Node(5);
root->left = new AVLTree::Node(3);
root->right = new AVLTree::Node(10);
root->left->left = new AVLTree::Node(2);
root->left->right = new AVLTree::Node(4);
root->right->left = new AVLTree::Node(7);
root->right->right = new AVLTree::Node(11);
root->left->left->left = new AVLTree::Node(1);
root->right->left->left = new AVLTree::Node(6);
root->right->left->right = new AVLTree::Node(9);
root->right->right->right = new AVLTree::Node(12);
root->right->left->right->left = new AVLTree::Node(8);
AVLTree tree(root);
cout << "Original Tree (in-order): ";
tree.printTree();
// 특정 값을 삭제
tree.deleteValue(10);
cout << "Tree after deleting 10 (in-order): ";
tree.printTree();
return 0;
}- 이진탐색트리는 좌우로 숫자의 대소는 확실하게 비교할 수 있으나, 들어가는 순서에 따라서 트리가 쓸데없이 길어질 수 있다는 단점이 있었다. 즉 탐색은 성공하더라도 그 시간이 너무 길어질 수 있었다. 한쪽으로 부모자식노드가 치우친다거나 하는식으로 말이다.
- AVL트리는 balance factor라는 요소를 넣어서 저울 처럼 좌 우 중 한쪽의 차수가 2 이상 높을때 재조정하도록 하는 트리이다. 이로써 최대 차수를 낮추고 최악의 경우 길어지는 탐색시간을 줄인다.
- 그 균형을 맞추는 기본 아이디어는 회전이다. 한쪽의 차수가 2보다 높을때 다음과 같은 회전을 따른다.

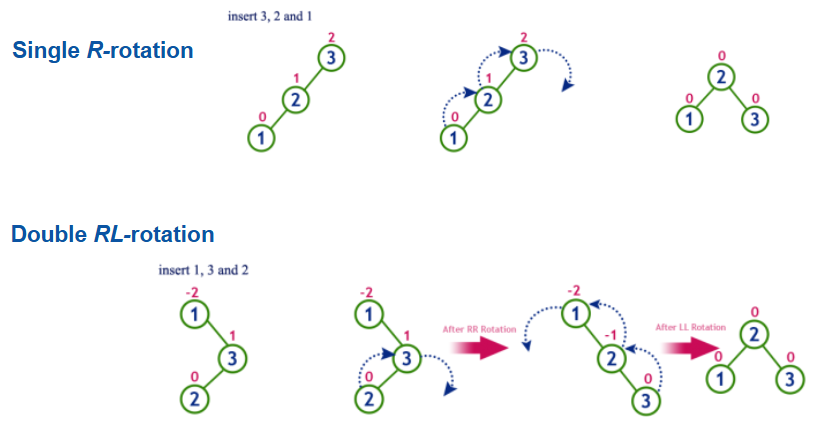
- single rotation일때 기존 2번 노드에 붙어있던 자식노드가 문제가 될 수도 있다. 이 경우 가장 위에있던 노드의 자식으로 붙여준다고 생각하면 된다.
- 노드를 중간에 삭제할때는 삭제된 노드의 왼쪽 자식서브트리의 값중 가장 큰 값이나 오른쪽 자식 서브트리의 값중 가장 작은 값이 그 위치를 대체하고 이후에 위에서부터 재조정한다.
Red-black Tree
- Red-black 트리는 이진 탐색트리의 일종으로 기본 규칙은 다음과 같다.
-
- 각 노드들은 red 나 black 색깔을 가지게 된다.
- root는 검정이고 모든 NULL 잎도 검정이다.
- 빨강 노드의 자식은 모두 검정이다.
- 모든 경로에서 검정노드의 개수는 동일해야 한다.(이를 검정 높이라고 함)
- 만약 자식이 모두 red라면 부모를 red로 바꾸고 자식은 black으로 전환한다.
- black 부모는 하나의 black 자식만을 가질 수 없다.
-
- 삽입 과정
- 새로운 노드를 빨강으로 삽입:
- 새 노드는 항상 **빨강(Red)**으로 삽입됩니다.
- 삽입 위치는 이진 탐색 트리의 규칙을 따라 결정합니다.
- 문제 탐지:
- 삽입된 노드의 부모가 **검정(Black)**이면 문제 없음 → 끝!
- 삽입된 노드의 부모가 **빨강(Red)**이면 규칙 위반 발생 → 수정 필요.
- 수정 작업:
- Case 1: 삼촌 노드도 빨강
→ 부모와 삼촌을 검정으로, 조부모를 빨강으로 변경.
→ 조부모를 기준으로 다시 규칙을 검사. - Case 2: 삼촌 노드가 검정 (또는 NULL)
→ 회전을 통해 균형을 맞춤:- Zig-Zag (삼각형): 먼저 작은 회전(부모 중심) 후 색 변경
- Zig-Zig (직선형): 색 변경 후 큰 회전(조부모 중심).
- Case 1: 삼촌 노드도 빨강
- 루트는 항상 검정:
- 수정 후, 루트가 빨강이면 검정으로 변경.
- 새로운 노드를 빨강으로 삽입:
- 삭제과정
- 노드 삭제:
- 삭제 위치는 일반적인 이진 탐색 트리의 삭제 규칙을 따릅니다:
- 삭제할 노드가 자식이 없으면 바로 제거.
- 삭제할 노드가 하나의 자식을 가지면 그 자식으로 대체.
- 삭제할 노드가 두 자식을 가지면, 후계자 노드(중위 순회 기준 바로 뒤 노드)를 찾아 대체한 뒤, 후계자를 삭제.
- 삭제 위치는 일반적인 이진 탐색 트리의 삭제 규칙을 따릅니다:
- 문제 탐지:
- 삭제된 노드가 빨강이면 문제 없음 → 끝!
- 삭제된 노드가 검정이면 규칙 위반 발생 → 수정 필요.
- 수정 작업:
-
- Case 1: Sibling이 RED
- 형제 노드(Sibling)가 RED라면:
- 부모와 형제의 색을 교환.
- 부모를 기준으로 회전.
- 이후, Double Black 문제를 Case 2, 3, 4로 재귀적으로 처리.
- 형제와 형제의 자식들이 모두 BLACK:
- 형제를 RED로 바꾼다.
- 부모 노드를 Double Black으로 승격.
- 재귀적으로 부모에서 문제를 해결.
- 형제의 가까운 자식(왼쪽 자식)이 RED:
- 형제와 가까운 자식의 색을 교환.
- 형제를 기준으로 회전.
- 문제를 Case 4로 변환.
- 형제의 먼 자식(오른쪽 자식)이 RED:
- 형제와 부모의 색을 교환.
- 부모를 기준으로 회전.
- 형제의 먼 자식을 BLACK으로 설정.
- Double Black 문제 해결 완료.
- 형제 노드(Sibling)가 RED라면:
- Case 1: Sibling이 RED
-
- 루트는 항상 검정:
- 수정 후, 루트가 빨강이면 검정으로 변경.
- 노드 삭제:
- 워낙 규칙이 복잡해서 외우진 않았다....
2-3 Tree
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class TwoThreeTree {
public:
struct Node {
vector<int> keys; // 노드에 저장된 키들
vector<Node*> children; // 자식 노드들
Node(int key) {
keys.push_back(key);
}
// 리프 노드인지 확인
bool isLeaf() {
return children.empty();
}
// 노드가 가득 찼는지 확인
bool isFull() {
return keys.size() == 2;
}
};
Node* root;
TwoThreeTree() : root(nullptr) {}
// 트리 출력 함수
void printTree(Node* node, string indent = "", bool last = true) {
if (!node) return;
cout << indent;
if (last) {
cout << "└── ";
indent += " ";
} else {
cout << "├── ";
indent += "| ";
}
for (int key : node->keys)
cout << key << " ";
cout << endl;
for (size_t i = 0; i < node->children.size(); i++)
printTree(node->children[i], indent, i == node->children.size() - 1);
}
void print() {
printTree(root);
}
// 삽입 함수
void insert(int key) {
if (!root) {
root = new Node(key);
} else {
Node* newChild = insertInternal(root, key);
if (newChild) {
// 루트 분할이 발생
Node* newRoot = new Node(newChild->keys[0]);
newRoot->children.push_back(root);
newRoot->children.push_back(newChild);
root = newRoot;
}
}
}
private:
// 내부 삽입 함수
Node* insertInternal(Node* node, int key) {
if (node->isLeaf()) {
node->keys.push_back(key);
sort(node->keys.begin(), node->keys.end());
if (node->isFull()) {
return split(node);
}
return nullptr;
} else {
Node* childToInsert = findChild(node, key);
Node* newChild = insertInternal(childToInsert, key);
if (newChild) {
insertIntoParent(node, newChild);
if (node->isFull()) {
return split(node);
}
}
return nullptr;
}
}
// 노드 분할
Node* split(Node* node) {
Node* newNode = new Node(node->keys[1]);
node->keys.erase(node->keys.begin() + 1);
if (!node->isLeaf()) {
newNode->children.push_back(node->children[2]);
newNode->children.push_back(node->children[3]);
node->children.erase(node->children.begin() + 2, node->children.end());
}
return newNode;
}
// 자식 노드를 찾아주는 함수
Node* findChild(Node* node, int key) {
if (key < node->keys[0]) return node->children[0];
if (node->keys.size() == 1 || key < node->keys[1]) return node->children[1];
return node->children[2];
}
// 부모 노드에 새 자식을 삽입
void insertIntoParent(Node* parent, Node* child) {
int newKey = child->keys[0];
parent->keys.push_back(newKey);
sort(parent->keys.begin(), parent->keys.end());
auto it = find(parent->keys.begin(), parent->keys.end(), newKey);
size_t index = distance(parent->keys.begin(), it);
parent->children.insert(parent->children.begin() + index + 1, child);
}
};
int main() {
vector<int> input = {59, 76, 43, 94, 29, 97, 30, 77, 49, 12, 41, 69, 29, 22, 13, 18, 82, 5};
TwoThreeTree tree;
cout << "Inserting elements into the 2-3 Tree...\n";
for (int num : input) {
tree.insert(num);
cout << "Inserted " << num << ":\n";
tree.print();
cout << "-----------------\n";
}
cout << "Final 2-3 Tree structure:\n";
tree.print();
return 0;
}- 2-3 트리는 노드당 값이 1개, 자식노드는 2개까지 가질수 있었던 이진트리와는 다르다.
- 1개의 키와 2개의 자식을 가지는 기존 2노드와 2개의 키와 3개의 자식을 가지는 3노드가 모두 가능하다.
- 즉 자식노드 3개는 부모 노드의 키에 따라 2개의 키보다 작은지, 그 사이에 있는지, 그 둘 모두보다 큰지에 따라 위치가 결정된다.
- 삽입 과정
- 삽입 위치 탐색:
- 새 키가 들어갈 리프 노드를 찾습니다. 이때 기존 이진트리처럼 새로운 노드로 가는게 아니라 기존 잎 노드로 들어가게 된다.
- 삽입 후 처리:
- 리프 노드가 2노드인 경우:
- 새 키를 추가하여 3노드로 만듭니다.
- 리프 노드가 3노드인 경우:
- 키를 삽입한 뒤 **분할(Split)**을 수행합니다:
- 가운데 키는 부모 노드로 올라가고, 나머지 키는 두 개의 자식 노드로 나뉩니다.
- 부모 노드도 3노드가 되면 추가적으로 분할이 발생할 수 있습니다.
- 키를 삽입한 뒤 **분할(Split)**을 수행합니다:
- 리프 노드가 2노드인 경우:
- 삽입 위치 탐색:
- 삭제 과정
- 삭제 위치 탐색:
- 삭제할 키가 리프에 있는 경우 바로 삭제.
- 삭제할 키가 내부 노드에 있는 경우:
- 후계자(오른쪽 서브트리에서 가장 작은 키) 또는 선행자(왼쪽 서브트리에서 가장 큰 키)로 교체한 뒤 삭제.
- 균형 조정:
- 삭제로 인해 노드가 비게 되면, **재배치(Restructure)**나 **병합(Merge)**이 발생.
- 부모와 형제 노드에서 키를 빌리거나 병합하여 트리의 균형을 유지.
- 삭제 위치 탐색:
B-Tree
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class BTree {
public:
struct Node {
vector<char> keys;
vector<Node*> children;
bool isLeaf;
Node(bool leaf) : isLeaf(leaf) {}
};
Node* root;
int t; // 차수 (최소 자식 노드 수)
BTree(int degree) : t(degree), root(nullptr) {}
// 삽입 함수
void insert(char key) {
if (root == nullptr) {
root = new Node(true);
root->keys.push_back(key);
} else {
if (root->keys.size() == 2 * t - 1) {
Node* newNode = new Node(false);
newNode->children.push_back(root);
split(newNode, 0);
root = newNode;
}
insertNonFull(root, key);
}
}
// 노드 분할 함수
void split(Node* parent, int i) {
Node* fullNode = parent->children[i];
Node* newNode = new Node(fullNode->isLeaf);
char median = fullNode->keys[t - 1];
parent->keys.insert(parent->keys.begin() + i, median);
parent->children.insert(parent->children.begin() + i + 1, newNode);
newNode->keys.assign(fullNode->keys.begin() + t, fullNode->keys.end());
fullNode->keys.resize(t - 1);
if (!fullNode->isLeaf) {
newNode->children.assign(fullNode->children.begin() + t, fullNode->children.end());
fullNode->children.resize(t);
}
}
// 자식이 가득 찬 노드에 키 삽입
void insertNonFull(Node* node, char key) {
int i = node->keys.size() - 1;
if (node->isLeaf) {
while (i >= 0 && key < node->keys[i]) {
i--;
}
node->keys.insert(node->keys.begin() + i + 1, key);
} else {
while (i >= 0 && key < node->keys[i]) {
i--;
}
i++;
if (node->children[i]->keys.size() == 2 * t - 1) {
split(node, i);
if (key > node->keys[i]) {
i++;
}
}
insertNonFull(node->children[i], key);
}
}
// 트리 출력 함수
void print(Node* node, int level = 0) {
if (node == nullptr) return;
cout << string(level, '-') << " ";
for (char key : node->keys) {
cout << key << " ";
}
cout << endl;
if (!node->isLeaf) {
for (Node* child : node->children) {
print(child, level + 1);
}
}
}
void display() {
print(root);
}
};
int main() {
// 차수가 5인 B-Tree 생성
BTree tree(5);
// 주어진 입력값
vector<char> values = {'y', 'a', 'g', 'f', 'b', 'k', 'd', 'h', 'm', 'j', 'e', 's', 'r', 'x', 'c', 'l', 't', 'u', 'v', 'w', 'o', 'i', 'z', 'n', 'q', 'p'};
// 값 삽입
for (char val : values) {
tree.insert(val);
}
// 최종 B-Tree 출력
cout << "Final B-Tree:" << endl;
tree.display();
return 0;
}- 2-3트리가 포함되는 개념으로 m-1개의 키와 최소 m/2개의 자식을 가질 수 있는 트리이다. (단 루트노드의 자식이 2개이상일 필요는 없다.)
- 여전히 2-3트리와 유사한 규칙을 가진다. 여기서는 차수가 5인경우 그러니까 최대 4개의 키와 최소 2개의 자식노드를 가지는 경우로 설명하겠다.
- 여전히 4개의 최대 4개의 키를 가지고 5개 이상이면 그 노드는 문할된다. 중앙값을 부모 노드에 삽입한다.
- 삭제는 단말에서만 삭제가 가능하니 삭제될 노드를 잎으로 이동시킨후 삭제한다.
Heap sort
#include <iostream>
#include <vector>
using namespace std;
// 힙 구조를 만족하도록 배열을 조정하는 함수
void heapify(vector<int>& arr, int n, int i, bool isMaxHeap) {
int extreme = i; // 루트
int left = 2 * i + 1; // 왼쪽 자식
int right = 2 * i + 2; // 오른쪽 자식
// 부모와 왼쪽 자식 비교 (최대 힙 or 최소 힙에 맞게)
if (left < n) {
if ((isMaxHeap && arr[left] > arr[extreme]) || (!isMaxHeap && arr[left] < arr[extreme])) {
extreme = left;
}
}
// 부모와 오른쪽 자식 비교 (최대 힙 or 최소 힙에 맞게)
if (right < n) {
if ((isMaxHeap && arr[right] > arr[extreme]) || (!isMaxHeap && arr[right] < arr[extreme])) {
extreme = right;
}
}
// 최댓값 또는 최솟값이 루트가 아니라면 값을 교환하고, 재귀적으로 heapify
if (extreme != i) {
swap(arr[i], arr[extreme]);
heapify(arr, n, extreme, isMaxHeap);
}
}
// 힙 정렬 함수
void heapSort(vector<int>& arr, bool isMaxHeap) {
int n = arr.size();
// 힙을 구성 (배열을 힙으로 만들기)
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i, isMaxHeap);
}
// 힙에서 최대값 또는 최소값을 추출하여 배열의 끝과 교환 후 다시 힙ify
for (int i = n - 1; i > 0; i--) {
swap(arr[0], arr[i]); // 최대값/최소값을 배열의 끝으로 이동
heapify(arr, i, 0, isMaxHeap); // 힙 사이즈가 하나 줄었으므로 다시 힙ify
}
}
int main() {
vector<int> arr = {82, 45, 37, 59, 68, 19, 34, 27, 98, 11, 52, 77, 49, 25, 64, 15, 90, 30, 88, 73, 50, 33, 92, 61, 80, 57, 39, 21, 94, 13, 60, 48, 53, 18, 95, 74, 67, 72, 87, 100};
// 최대 힙을 이용한 내림차순 정렬
vector<int> maxHeapArr = arr; // 배열 복사
cout << "Max Heap Sort (Descending): ";
heapSort(maxHeapArr, true); // 최대 힙으로 정렬
for (int num : maxHeapArr) {
cout << num << " ";
}
cout << endl;
// 최소 힙을 이용한 오름차순 정렬
vector<int> minHeapArr = arr; // 배열 복사
cout << "Min Heap Sort (Ascending): ";
heapSort(minHeapArr, false); // 최소 힙으로 정렬
for (int num : minHeapArr) {
cout << num << " ";
}
cout << endl;
return 0;
}- 힙은 이진 탐색 트리와 유사하게 생겼지만 아예 다르다.
- 이진 탐색트리는 숫자의 대소관계를 좌우에 따라 구별하였지만, 힙은 상하(부모,자식노드)로 구별한다.
- 즉 가장 큰 값이나 가장 작은 값이 root 자리에 오고 서브트리들도 그 대소규칙을 따른다.
- 그래서 최대나 최소값을 이용해 가장 작은값이나 가장 큰값이 먼저와 우선순위 큐를 구현할때 쓴다.
- 힙은 특이하게 기존의 트리들이 포인터로 주로 구현했던것과 달리 배열을 이용한다. 완전 이진트리여서 나누기 2하면 부모의 위치가 나오기 때문이다.
- 배열을 힙으로 바꾸는 과정
- 일단 배열을 이진트리 형태로 쭉 넣는다.
- 루트 노드 부터 자식노드(자신의 index *2, index*2+1)과 비교하며 swap 한다.
- 힙의 삭제과정
- 힙은 접근도 root만 되기 때문에 삭제도 root만 된다.
- root 노드를 삭제하면 그 자리는 가장 아래의 가장 오른쪽 노드를 가져온다.
- 그 후 다시 재배열 하는 heapify 과정을 거친다.
Least common multiple
#include<iostream>
int gcd(int a, int b){
if(a>b){
if(a%b==0){
return b;
}
else{
return gcd(b,a%b);
}
}
else{
if(b%a==0){
return a;
}
else{
return gcd(a,b%a);
}
}
}
int lcm(int a, int b){
return a*b / gcd(a,b);
}
int main(){
int m,n;
scanf("%d %d",&m,&n);
printf("%d",lcm(m,n));
return 0;
}- 최소공배수를 구하는 알고리즘으로 소인수분해 없이도 편한 방법으로 구할 수 있다.
- 두 수의 곱은 그 두 수의 최대공약수와 최소공배수의 곱과 같다는 접근을 이용한다.
- 두 수는 이미 주어졌고. 유클리드 알고리즘으로 최대공약수를 빠르게 구할 수 있으므로 최대공배수도 그만큼 빠르게 구할 수 있다.
결론
Transform and Conquer에 관한 알고리즘들이었다.
이어지는 내용
[알고리즘] 5. Greedy Method 내용 정리
1. Brute force2. Divide and conquer3. Decrease and conquer4. Transform and conquer5. Greedy Method6. Dynamic Programming7. Backtracking8. Branch and Bound여기서는 Greedy Method 에 대해 다룬다. Greedy method란그리디 알고리
juneforpay.tistory.com