[백준] 11660번: 구간 합 구하기 5 풀이 및 해설(C++)
풀이
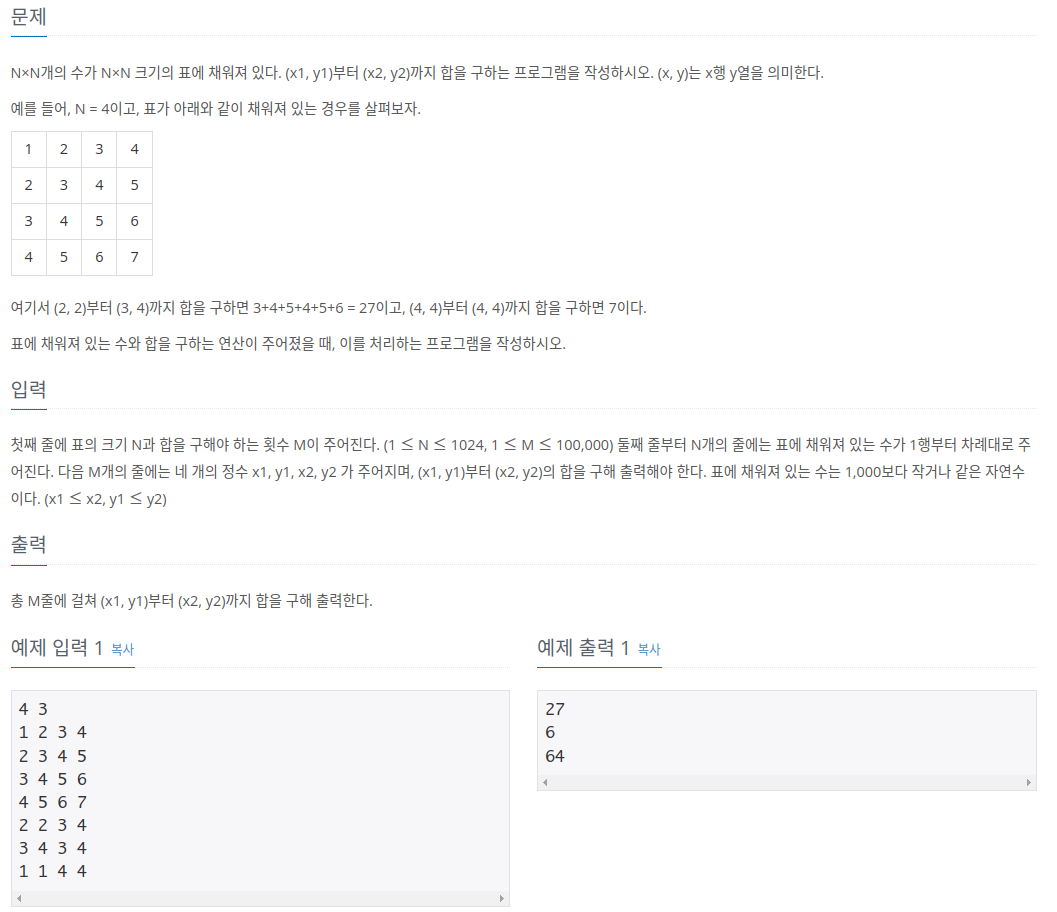
숫자가 들어있는 직사각형 표가 주어진다. 그리고 주어진 표에서 직사각형모양으로 수를 선택할 때 그 직사각형 안 수들의 합을 구하라는 문제다. 반복문을 통해 그때그때 답을 구하게 된다면 큰 수가 주어졌을 때 시간초과가 날 것이다. 최대로 계산하는 경우는 1024*100,000으로 대략 10억 번이다. 그런데 문제 제한 시간은 1초로 초당 1억 번 정도 계산한다고 치면 시간초과가 나는 것이다.
그래서 우리는 이 문제를 동적계획법을 이용한 합으로 계산할 것이다.
sum 배열에는 0,0 부터 그 위치를 꼭짓점으로 하는 직사각형을 그리고 그 합을 저장한다.
가령 sum[1][3]에는 arr [0][0], arr [0][1], arr [0][2], arr [0][3], arr [1][0], arr [1][1], arr [1][2], arr [1][3]의 합이 들어있다.
문제에서 요구한 합을 구하기 위해서는 어떻게 해야할까? 문제에서 (a, b)부터 (c, d)까지의 합을 구하라고 했다고 가정하자.
(a <=c, b <=d)
sum(c, d)에서 sum(a-1,d) 를 빼면 가로는 a~c, 세로는 0~d까지 직사각형 모양의 arr 수열의 합이다.
sum(c,d) 에서 sum(c, b-1)를 빼면 가로는 0~c, 세로는 b~d까지 직사각형 모양의 arr 수열의 합이다.
sum(c, d)에서 sum(a-1, d)와 sum(c, b-1)를 빼고, sum(a-1, d)와sum(c, b-1)에서 중복으로 빼진 sum(a-1, b-1)을 더하면
가로는 a~c, 세로는 b~d까지 직사각형 모양의 arr 수열의 합이 나온다.
즉 답은 sum(c, d)-sum(a-1, d)-sum(c, b-1)+sum(a-1, b-1)이다.
그렇다면 sum 배열은 어떻게 구할 수 있을까?
sum(x, y)를 구해야 된다고 할 때 마찬가지 원리로 sum(x, y)=sum(x-1, y)+sum(x, y-1)-sum(x-1, y-1)+arr [x][y]로 구할 수 있다.
해답 코드
#include <iostream>
#define fastio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
int main(){
fastio;
int n,m,x1,x2,y1,y2;
cin>>n>>m;
int arr[n+1][n+1]={0};
int sum[n+1][n+1]={0};
for(int i=1; i<n+1; i++){
for(int j=1; j<n+1; j++){
cin>>arr[i][j];
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+arr[i][j];
}
}
for(int i=0; i<m; i++){
cin>>x1>>y1>>x2>>y2;
cout<<sum[x2][y2]+sum[x1-1][y1-1]-sum[x2][y1-1]-sum[x1-1][y2]<<'\n';
}
}
PLUS
다이내믹 프로그래밍과 수열 발상이 중요한 문제였다.